NAMA : MAYA
KELAS : Xl MIPA 3
Suku banyak atau polinomial merupakan bentuk aljabar yang memuat suatu variabel. Oleh karena itu, suku banyak bisa kita tulis dalam bentuk fungsi dari variabelnya. Misalnya, suku banyak dengan variabel x dapat kita tulis sebagai fungsi dari x (f(x)).

Syarat Polinomial
Terdapat juga beberapa syarat sehingga sebuah persamaan bisa disebut sebagai ‘polinomial’, diantaranya ialah sebagai berikut:
•Variabel tidak boleh mempunyai pangkat pecahan atau negatif.
•Variabel tidak boleh masuk dalam sebuah persamaan trigonometri.
Nilai Polinomial
Nilai polinomial f(x) untuk x=k atau f(k) dapat kita cari dengan menggunakan metode substitusi atau dengan skema Horner. Berikut rinciannya:
Cara subtitusi:
Dengan mensubtitusikan x = k ke dalam polinomial, sehingga akan menjadi:
f(x) = an kn + an-1 kn-1 + . . . + a1 k + a
Cara skema horner:
Sebagai contoh:
(f(k) = x3 + bx2 + cx + d maka: f(k) = ak3 + bk2 + ck + d
xa3 + bx2 + cx + d = (ak2 + bk + c)k+d
= ((ak + b)k + c)k+d
Pembagian polinomial
Secara umum, pembagian dalam polinomial dapat dituliskan seperti di bawah ini:
Rumus: f(x) = g(x) h(x) + s(x)
Keterangan:
f(x) merupakan suku banyak yang dibagi.
g(x) merupakan suku banyak pembagi.
h(x) merupakan suku banyak hasil bagi.
s (x) merupakan suku banyak sisa.
1. Metode Pembagian Biasa
Contohnya adalah jika 2×3 – 3×2 + x + 5 dibagi dengan 2×2 – x – 1
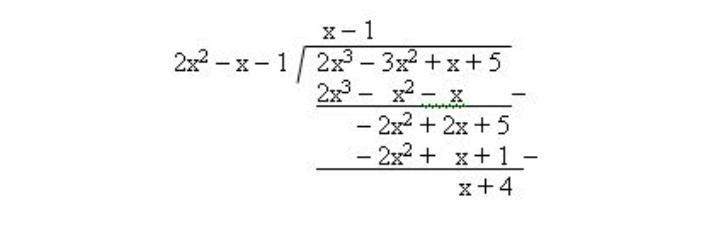
maka hasil bagi dan sisanya adalah hasil bagi = x-1 dan sisa = x+4
2. Metode Horner
Metode ini dipakai untuk pembagi yang berderajat 1 ataupun pembagi berderajat n yang bisa difaktorkan jadi pembagi-pembagi dengan derajat 1.
Langkah langkah :
1) Tulis koefisien dari polinomialnya → harus urut dari koefisien xn, xn – 1, … hingga konstanta (untuk variabel yang tidak memiliki koefisien, maka ditulis 0). Misalkan untuk 5×3 – 8, koefisien-koefisiennya adalah 5, 0, 0, dan -8
2) Untuk koefisien dengan derajat tertinggi P(x) ≠ 1, hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
3) Jika pembagi dapat difaktorkan menjadi
P1 dan P2, maka S(x) = P1 × S2 + S1
P1, P2, P3, maka S(x) = P1×P2×S3 + P1×S2 + S1
P1, P2, P3, P4, maka S(x) = P1×P2×P3×S4 + P1×P2×S3 + P1×S2 + S1
dan seterusnya
Untuk lebih jelasnya, mari simak contoh berikut ini
Misalkan diketahui
F(x) = 2×3 – 3×2 + x + 5
P(x) = 2×2 – x – 1
Tentukan hasil bagi dan sisanya
Jawab :
F(x) = 2×3 – 3×2 + x + 5
P(x) = 2×2 – x – 1 = (2x + 1)(x – 1)
Sehingga p1 : (2x + 1) = 0 -> x = -1/2 dan p2 : (x – 1) = 0 -> x = 1
Kemudian langkah hornernya ditunjukkan pada gambar berikut
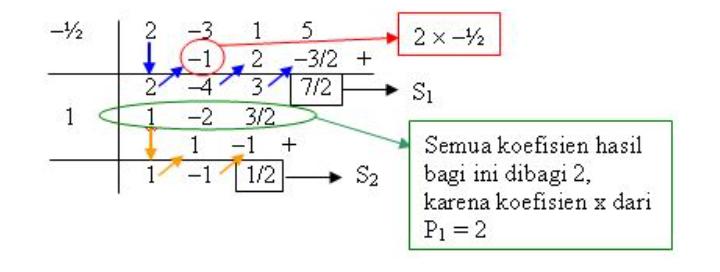
H(x) = x-1
S(x) = P1×S2 + S1 = x + 4
Contoh soal polinomial 1

Contoh soal polinomial 2
